How the algorithm works

This documents explains the basic ideas behind the different solvers and gives some tips to improve the results and get faster results.

Data analysis

Creation of funObj

As explained in model creation, the program tries to find the best parameters that minimize the error between some experiments and models. In order to do so models need to be designed to mimic the experiment.

The data obtained in each simulation ran in the models is directly compared with the appropriate experimental curve. For this purpose you need to specify the axis limits and number the points so only that segment is used. Maybe the models don’t work well after a point or the experiment is only valid between a region, this way you can set that.

It is important to note that only the segment written will be used to compare the data. This means that everything you see in the graphs is exactly the same that the algorithm is seeing. If you have bad steady-state values for example it could be a good idea to increase the range so you give the algorithm more steady-state points.

Besides that the data is compared to create an average error used as an objective function. The function to calculate the error at one point used is:

Basically the difference between model and experiment at any point is divided by a divisor that is the experiment value if this is bigger than a certain percentage p of the mean of all the values in that experiment. This is done so that for small values the error is not amplified.

Each error of the model is added together for the whole experiment and scaled as follow:

Finally the error of each model is added together and scaled by the number of curves:

This makes that at the end the objective function defined in funObj.m will give an error that is the average error between all the models respecting that if a model has a lot of points it will not matter more than one with less.

Scaling of parameters

It is always a good idea to scale the parameters. In the application there are two types of scaling: linear and logarithmic. By default variables are scaled linearly unless otherwise specified. The way it works is:

· Linear: The parameter is scaled by the absolute value of the initial guess. For the limits the same is done also with the initial guess value.

· Logarithmic: The parameter is transformed into as well as its limits.

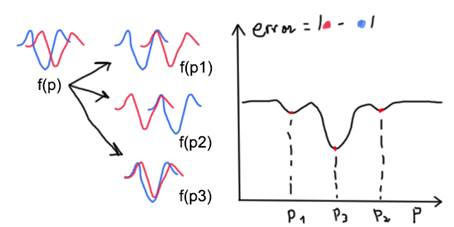
Usually the linear transformation is fine. The logarithmic one is designed for the event of parameters that can change in orders of magnitudes. You can mix linear and log transformations in the same simulation but it is important to note that there may be problems if a linear constraint includes both linear and logarithmic parameters.

When you scale the parameters the algorithm used to solve the minimization problem will see all the parameters similar. This is useful because parameters that change a lot from one to another are harder to estimate as there may be rounding error issues. Also there may be problem with the estimation of gradients. This issue is solved with the scaling which is done automatically.

How the algorithms work

Two main group of algorithms have been selected as possible ones to solve the optimization problem:

· Gradient-based: This methods will perturb the parameters to estimate the gradient of the system at the current point as the difference between the errors with respect to the perturbation in a parameter. With this information and taking into account the constraints by creating logarithmic barriers a simplified system (usually linear) is done and used to estimate the optimum change in the parameters based in its simplified behavior. This methods work well with continuous variables where all the points are defined and there are no strange changes in their values. It works best with linear problems but can be applied with good results to non-linear ones.

The algorithm will start with the initial values set and will estimate the gradients. Using this information it will move the parameters from the starting point to the place where it thinks it’s the best based in the simplified system created. This will usually move the parameters to somewhere where the funObj is minimized and thus the models and experiments are more similar. As a simplified model is created usually it will need more iterations to find the parameters that minimize the error. It will continue for the new starting point doing the same. Functions and parameters need to be continuous and need to be more or less smooth. If the functions have sudden changes or the parameters are discrete this method may not be used.

It is important to note that the final solution is dependent of the initial point set. If a function has several local minimums the algorithm will typically find the closest one from the starting point as illustrated below:

Imagine we want to find the shift p to move the red curve so it’s on top of blue. You can see that there are three different minimums and it can go to any of them. It is however more likely to go the one closer from the start point.

The shifts p1 and p2 represent local minimum and p3 a global minimum. The best solution is found in the global minimum and some algorithms are designed to try to find them and others not:

o Fmincon: It uses the gradient-based approach to find the closest set of parameters that minimize the error and thus only gives local minimums that may or may not be global minimums. However this is the fastest way to solve the problem and in most cases it is enough. More info at http://www.mathworks.com/help/optim/ug/fmincon.html.

o Global Search: It’s similar to fmincon but uses more than one starting point. The algorithm will use an optimum scatter pattern to auto-generate more starting points. Then it will pick the best ones to use as stage 1 points in fmincon. If enough points are chosen it is likely to find the global minimum. However as more starting points are used the number of iterations grow and this method is only recommended if fmincon gives bad results. More info at http://www.mathworks.com/help/gads/globalsearch-class.html.

· Genetic algorithms: They use a heuristic method that mimics evolution. They do not create approximations of the systems with gradients. What they do is to start with a big number of points and check their fitness which is related to the error they produce. From this starting point the algorithm will pick pairs of points to create new points sharing characteristics of the parents. It picks the parents based on the fitness so it’s more likely to use the best points to generate more. It also adds mutations which are sudden changes that are not present in the parents. With this idea it tries to find alternative ways that may be better and are not possible to obtain using only the parent’s information. It can be seen that this approach while it is generic and should work in most problems will be much slower than any gradient-based method. For example you can use this method with discrete functions or variables, undefined points, etc. More info: http://www.mathworks.com/help/gads/ga.html.

With all this information it is recommended to start with fmincon. If it doesn’t work you can try Global Search. If you can’t use a gradient-based method you may then use a genetic algorithm instead.

It is important to note that there are no methods that guarantee you have found a global minimum. Either global search, genetic algorithms or even any other method you may think of will not guarantee a global minimum. You can think of it like finding the lowest point in a surface when you’re blindfolded. The only way to guarantee you have found the lowest is to check every single step or to have great information about the system in which case you would not need a minimization method to begin with. For this reason always use reason to judge if the results obtained are appropriate.

Tips

Here is a list of tips to improve results and get faster convergences:

· You may combine as many circuits in the same model file because the time it takes to run a new circuit file is quite big. If you manage to run create a static test for different Vge for example in the same .cir it will decrease simulation time from the alternative of having a model for each Vge. Combining experimental data in the same .txt file does not produce noticeable improvements.

· You can try to put _log at the end of the parameter names that you expect to vary in order of magnitudes. You can try with and without to see the effect but basically for this parameters the estimations of gradients and so on will be greater as they get bigger and smaller as the get smaller and not constant. This makes sense as the degree of certainty is closely related to the power of the value. You wouldn’t expect to have a result of 100+-1e-6 but for 1e-5 to have a precision of 1e-6 it seems more appropriate. However if a parameter is not expected to change that much then this is not that important.

· It is complicated if not impossible to develop a pause button since the simulations are running Matlab optimization methods that do not support this option. For this reason, and to do more simulations at the same time the use of Virtual Machines is advised. You can create a Windows XP machine with Matlab and Pspice giving 20GB of space and only 1-1.5GB of ram. Also if you need to pause the simulation in theory you can just pause and resume the virtual machine. You may need to reconnect to the VPN and press no in the “use demo” message from Pspice but hat’s it. Also you must understand Matlab is only using a single core and I’m not sure about Pspice but still you may be able to run 4 simulations in a similar amount of time as one with the added bonus of pausing them.

· You can export results for later viewing and it will also save the configuration file in a .txt so you can recheck what you did exactly later. Also it will generate some .m files that if you inspect you can see you have access to raw data of the parameter changes as well as the final solution curves so you can use to save the images in any format you want.